Lösung der Aufgaben 1 und 2
Aufgabe 1:
Bilden Sie die erste Ableitung der Funktion f mit f(x)=(2x2+5)·e-2x.
(2 VP)
Aufgabe 2:Gegeben ist die Funktion f mit f(x)=4sin(2x).
Bestimmen Sie diejenige Stammfunktion von f mit F(π)=7.
(2 VP)
Aufgabe 3:Lösen Sie die Gleichung
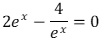 .
.
(3 VP)
Aufgabe 4:Gegeben sind die Funktionen fund g mit f(x)=-x2+3 und g(x)=2x.
Bestimmen Sie den Inhalt der Fläche, die von den Graphen der beiden Funktionen eingeschlossen wird.
(4 VP)
Aufgabe 5:Eine Funktion f hat folgende Eigenschaften:
(1) f(2)=1
(2) f'(2)=0
(3) f''(4)=0 und f'''(4)≠0
(4) Für x→+∞ und x→-∞ gilt f(x)→5
Beschreiben Sie für jede dieser vier Eigenschaften, welche Bedeutung sie für den Graphen von f hat.
Skizzieren Sie einen möglichen Verlauf des Graphen.
(5 VP)
Aufgabe 6:Die Gerade g verläuft durch die Punkte A(1|-1|3) und B(2|-3|0).
Die Ebene E wird von g orthogonal geschnitten und enthält den Punkt C(4|3|-8).
Bestimmen Sie den Schnittpunkt S von g und E.
Untersuchen Sie, ob S zwischen A und B liegt.
(4 VP)
Aufgabe 7:Gegeben sind die beiden Ebenen E1: 2x1-2x2+x3=-1 und
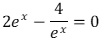 .
.Zeigen Sie, dass die beiden Ebenen parallel zueinander sind.
Die Ebene E3 ist parallel zu E1 und E2 und hat von beiden Ebenen denselben Abstand.
Bestimmen Sie eine Gleichung der Ebene E3.
(4 VP)
Aufgabe 8:a) Neun Spielkarten (vier Asse, drei Könige und zwei Damen) liegen verdeckt auf dem Tisch.
Peter dreht zwei zufällig gewählte Karten um und lässt sie aufgedeckt liegen.
Berechnen Sie die Wahrscheinlichkeit der folgenden Ereignisse:
A: Es liegt kein Ass aufgedeckt auf dem Tisch.
B: Eine Dame und ein Ass liegen aufgedeckt auf dem Tisch.
b) Die neun Spielkarten werden gemischt und erneut verdeckt ausgelegt.
Laura dreht nun so lange Karten um und lässt sie aufgedeckt auf dem Tisch liegen, bis ein Ass erscheint. Die Zufallsvariable X gibt die Anzahl der aufgedeckten Spielkarten an.
Welche Werte kann X annehmen?
Berechnen Sie P(X≤2).
(4 VP)
Aufgabe 9:Gibt es eine ganzrationale Funktion vierten Grades, deren Graph drei Wendepunkte besitzt? Begründen Sie Ihre Antwort.
(3 VP)
Lösung der Aufgaben 3 und 4
Lösung der Aufgaben 5 und 6
Lösung der Aufgabe 7
Lösung der Aufgaben 8 und 9